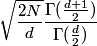level 11
人For我我For人
楼主
醉汉在二维平面上随机走N步,其中每步走单位长度,方向随机(从0到2pi都可取)。
问N步之后的位置与原点的距离的
1:距离平方的期望E[Dist^2]
2:距离期望的平方E[Dist]^2
众所周知,距离平方的期望是E[Dist^2]=N,但是期望的平方E[Dist]^2很难求,网络上几乎找不到资料。
不过我用计算机模拟出来的结果是,如果将期望除以sqrt(N),也就是E[Dist]/sqrt(E[Dist^2]),当N趋向于无穷大的时候(我取到了100000,做了大概上万次随机试验),这个比值趋向于一个定值,大概在0.88左右,然后我惊讶地发现,0.88是sqrt(pi)/2的前两位(如果极限真是这个值的话,看上去很合理对不对!)。。。
所以,请问吧里有没有大神能证明这个极限的。。。
2013年09月04日 14点09分
1
问N步之后的位置与原点的距离的
1:距离平方的期望E[Dist^2]
2:距离期望的平方E[Dist]^2
众所周知,距离平方的期望是E[Dist^2]=N,但是期望的平方E[Dist]^2很难求,网络上几乎找不到资料。
不过我用计算机模拟出来的结果是,如果将期望除以sqrt(N),也就是E[Dist]/sqrt(E[Dist^2]),当N趋向于无穷大的时候(我取到了100000,做了大概上万次随机试验),这个比值趋向于一个定值,大概在0.88左右,然后我惊讶地发现,0.88是sqrt(pi)/2的前两位(如果极限真是这个值的话,看上去很合理对不对!)。。。
所以,请问吧里有没有大神能证明这个极限的。。。