39个小球，其中有1个和其他38个重量不一样，用无码天平称
4次，找出这坏球并判定是轻了还是重了。

先来看看12个球的情况。
12个小球，其中有1个和其他11个重量不一样，用无码天平称3次，找出这异球并判定是是轻了还是重了。
这是一个经典数学问题。这道题难度相当大。
我相信，面对别人给出的详细解答，
第一，许多人读了一点后，就会望而却步，不想卒读；
第二，有耐心读的，多数人也还是不一定能读懂；
第三，即使读懂了，让他说给别人听，他大概是说不清楚；
第四，能说出来的，复述时也还是很困难。如果隔的时间长的话，也许他自己也要在重新思考中费劲地慢慢地说出。
我曾经就属于这类人。
具体地说，“12个球”问题，首先难在，解答难。第一次称后，如果
左右两边不平衡，应该怎么分组进行第二称，才能确保最后再称一次找出坏球并判定轻重。
其次难在，就算你得到了正确解答，但怎么让读者读懂。这相当难。
有关问题我在数学类贴吧上已参与多次讨论，重点是要探究怎么“
说清楚”，让读者明白。曾试用“
枝形图法”、“
列表法”，虽有所改进，但一直不尽人意。
近年来，采用了“
引理法”，自我感觉相当不错，且宜于
推到一般情况。

“
12个球”解说：引理法。
先看三个引理：
引理1：如果已知3个球中的坏球是重（或轻）的，那么，称1次即可。方法是：
任取其中2个称。如果平，则天平下面那个是坏球；如果不平，那么重（或轻）的那个是坏球；
引理2：如果已知4个球中有坏球但不知轻重，且另有不少于3个的好球，那么，称2次即可。方法是：
第一次，从4个中任取3个，与3个好球称；
第二次，
（1）如果平，那么4个中剩的那一个是坏球，它与好球称，即知是重或轻；
（2）如果不平，即可知坏球是重（或轻）的，那么转化为前述的引理1。
引理3：如果已有“左4重、右4轻”共8个球，且另有不少于3个的好球，那么，称2次即可。
方法是：按下述方法分组：左3重1轻、右3好1重，天平下面3轻1好。称2次如下 ：
（1）如果第一次“左、右平”，那么，第二次，天平下面中的“3轻”转化为前述的引理1；
（2）如果第一次“左重、右轻”，那么，第二次，左“3重”也转化为前述引理1；
（3）如果第一次“左轻、右重”，那么，第二次，在左1轻或右1重中，可任取其一与好球称即可。
有了以上引理，下面可很简单、明白地把“经过3次称量找出坏球”的过程说出：
第一次：把12个球平均分成3组，天平上，左、右各放4个，天平下面还有4个。
称后，以下三种情况，都再称2次即可。
第二、三次：
（1）如果“左、右平”，那么，坏球在“下面”4个里，转化为前述的引理2；
（2）如果“左4重、右4轻”，那么，转化为前述的引理3；
（3）如果“左4轻、右4重”，那么，类似于（2），也转化为前述的引理3。

表达有问题,应该先练语文.

下面深入分析一下4楼说的3个引理。
引理1：如果已知3个球中的坏球是重（或轻）的，那么，称1次即可。
不难推知：已知坏球轻重时，称2次最多可从9个球中找出；称3次最多可从27个球中找出，……一般地说，称
n次最多可从3^n个球中找出。
着重看引理2和引理3。
引理2：如果已知4个球中有坏球但不知轻重，且另有不少于3个的好球，那么，称2次即可。
引理3：如果已有“左4重、右4轻”共8个球，且另有不少于3个的好球，那么，称2次即可。
这里的“4”个球以及“左4重、右4轻”中的“4”，是关键的一个数，关键之处在于，
4=3+1。其中的3，是疑轻或疑重的，可由“另有
不少于3个的好球”确定或替换，然后利用上引理1。
那么问题是：这“
另有不少于3个的好球”有吗？有！在第一称后，不管左右两边平衡与否，都自然出来所需要的好球了。

为了解“
39个”问题，先看三个引理（重说“12个”问题中的三个引理，并且加以推广）。请
耐心阅读、细心思考。
引理1
（
1）如果已知3个球中的坏球是重（或轻）的，那么，称1次即可。
（
2）如果已知9个球中的坏球是重（或轻）的，那么，称2次即可。
方法是：任取其中6个，分放天平两边称。如果平，则天平下面3个是坏球；如果不平，那么重（或轻）的那3个是坏球，都转化为引理1（1）；
引理2
（
1）如果已知4个球中有坏球但不知轻重，且另有不少于3个的好球，那么，称2次即可。
（
2）如果已知13个球中有坏球但不知轻重，且另有不少于9个的好球，那么，称3次即可。
方法是：
第一次，在13个球中任取9个，与另有的9个好球放在天平两边上称；
第二次、第三次：
（1）如果平，那么坏球在13个中剩的那4个中，这4个与4个好球称，问题转化为引理2（1），再称2次即可；
（2）如果不平，即可知坏球在取的9个中，且知是重（或轻）的，那么转化为前述的引理1（2），也是再称2次即可。
引理3
（
1）如果已有“左4重、右4轻”共8个球，且另有不少于3个的好球，那么，称2次即可。
（
2）如果已有“左13重、右13轻”共26个球，且另有不少于9个的好球，那么，称3次即可。
方法是：按下述方法分组：左9重4轻，右9好4重，下9轻4好。称3次如下：
（1）如果“左、右平”，那么，天平下面中的“9轻”转化为前述的引理1（2），再称2次。
（2）如果“左重、右轻”，那么，左“9重”也转化为前述的引理1（2），再称2次。
（3）如果“左轻、右重”，那么，左4轻及右4重。这时转化前述的引理3（1），再称2次。
（要说明的是，这其中的关键在于，在分组中要出现“9重”、“9轻”和“4轻4重”。所以，一开始把
13个分解成9+4，这相当于“12个”问题中的
4=3+1）。

问题：
39个小球，其中有1个和其他38个重量不一样，用无码天平称
4次，找出这异球并判定是是轻了还是重了。
解：
一，先把
引理复述如下：
引理1 如果已知9个球中的坏球是重（或轻）的，那么，称2次即可。
引理2 如果已知13个球中有坏球但不知轻重，且另有不少于9个的好球，那么，称3次即可。
引理3 如果已有“左13重、右13轻”共26个球，且另有不少于9个的好球，那么，称3次即可。
二，
操作过程
第一次：把39个球平均分成3组，天平的左、右各放13个，天平下面还有13个。
称后，以下三种情况，都再称3次即可：
第二、三、四次：
第一种情况：如果“左、右平”，那么，坏球在天平下面13个里，转化为前述的引理2。
稍具体点说，就是：在天平下面13个中任取9个与9个好球称（第二次），不论是平衡与否，都再称2次，共4次；
“更具体点说”的内容，请参看7楼的引理2（2）。
第二种情况：如果“左13重、右13轻”，那么，转化为前述的引理3。
稍具体点说，就是：按下述方法分组：左9重4轻，右9好4重，下9轻4好。称一下（第二次），无论是“平衡”、“左轻、右重”或“左重、右轻”，都再称2次，共4次；
“更具体点说”的内容，请参看7楼的引理3（2）。
第三种情况：如果“左13轻、右13重”，那么，也转化为前述的引理3。类似（2）。

前面解决了两个具体问题：一是，
12个球时，称
3次可找出且判定其轻重的坏球；二是，
39个球时，称
4次可找出且判定其轻重的坏球。
不难验证，所有
不多于12个球时，都可以
3次确保找出且判定其轻重的坏球；所有
不多于39个球时，都可以
4次确保找出且判定其轻重的坏球。
此类问题，实际上可
一般
地叙述为：
用天平称
n次，最多能从多少个球中确保找出且判定其轻重的坏球
。
“12个球”的问题，就应该改为：用天平称
3次，最多能从多少个球中确保找出且判定其轻重的坏球。答案是
12；
“39个球”的问题，就应该改为：用天平称
4次，最多能从多少个球中确保找出且判定其轻重的坏球。答案是
39。
如果理解、掌握了前面关于“12个球”、“39个球”的解答，就不难解答下面
问题：
（
1）用天平称
5次，最多能从多少个球中确保找出且判定其轻重的坏球。
（
2）请简单说说操作过程。

13楼
问题：
（1）用天平称
5次，最多能从多少个球中确保找出且判定其轻重的坏球。
（2）请简单说说操作过程。
重新看看三个引理（见7楼），认真体会其中真谛。
解说：
以前已经说过，引理2和引理3中，都有“
4=3+1”、“
13=9+4”。这表示的是“
混合编组”方式。我们分析一下表达方式：
“
3次问题”中，
1
+3
=4。这里边的3，是3的一次方。这里的
4的3倍=12，就是“称
3次最多能从
12个球中确保找出且判定其轻重的坏球”；
“
4次问题”中，
4+9=13。这里的4，就是上式的4，而9是3²；这里的
13的3倍=39，就是“称
4次最多能从
39个球中确保找出且判定其轻重的坏球”；
那么，“
5次问题”，就应该是
13+3³=40。这里的40的3倍=120，就是“称
5次最多能从
120个球中确保找出且判定其轻重的坏球”。
具体操作过程是：
第一次，左40、右40 、下40，
第二次及
第三、四、五次：
（1）如果“左、右平”，那么坏球在天平下面40个里，取其中27个与好玩球称（第二次），不论是平衡与否，都再称3次，共5次；
（2）如果“左40重、右40轻”，那么，按下述方法分组：左27重13轻，右27好13重，下27轻13好。称一下（第二次），不论是“平衡”、“左轻、右重”或“左重、右轻”，都再称3次，共5次；；
（3）如果“左40轻、右40重”，显然与（2）类似。

一般问题：用天平称
n次，能从多少个球中确保找出且判定其轻重的坏球。
前面已经解决的是：
称
3次：最多
12个球；
称
4次：最多
39个球；
称
5次：最多
120个球。
并且明确了具体的操作过程，这在
三个引理中得以体现。此外还探究了其中的数据的内在关系。
由“3次：12”、“4次：39”、“5次：120”我们看到一种“
递推”过程，也就是：
一，“混合分组”的数据组合：1+3^1=4、4+3²=13、13+3³=40。
二，“最大个数”的计算：3×（12+1）=39；3×（39+1）=120。
由此我们可得到：
称
6次：“混合分组”的数据组合为
40+3^4=121，“最大个数”为3×（120+1）=
363；
称
7次：“混合分组”的数据组合为
121+3^5=364，“最大个数”为3×（363+1）=
1092；
称8次、称9次……，在此不赘述了。

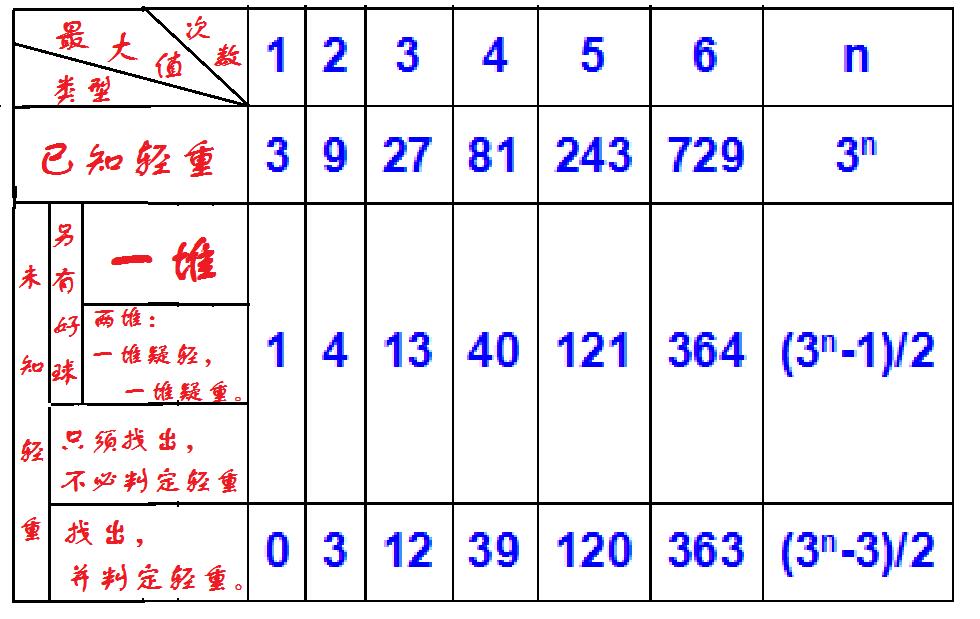
回过头来看看称1次、称2次能从多少个球中确保找出且判定其轻重的坏球。容易知道：
称
1次：
无；
称
2次：
3个球。

那么，一般的叙述是什么样的呢？

一般问题：用天平
称n次，
最多能从多少个球中确保找出且判定其轻重的坏球。
前面已经解决的是：
称
1次：
无；
称
2次：
3个球;0+1=1
称
3次：最多
12个球；“混合分组”的数据组合：1+3=4；
称
4次：最多
39个球；“混合分组”的数据组合：4+9=13；
称
5次：最多
120个球。“混合分组”的数据组合：13+27=40。
称
6次：最多
363个球；“混合分组”的数据组合为40+81=121，
称
7次：最多
1092个球；“混合分组”的数据组合为121+243=364，
现在来看看
一般情况下，
称n次的相关数据及相互关系。

有了前面对“
12球”、“
39球”的解说，又有了对一般情况的叙述，我们可以正式地提出问题、证明之、明确具体的操作过程了。
问题：m个小球，其中有1个和其他(m-1)个的重量不一样，用无码天平称n次，求可“找出这坏球并判定是轻了还是重了”了
最大值。
先看三个引理：
说明：要具体理解这些内容，请参看前面“
12球”、“
39球”的解说：当时也说的“三个引理”，尤其是“具体操作过程”。而本定理的一般证明，可运用
数学归纳法。

有了上述的定理，有了“12球”、“39球”的实际操作经验，我们就可以对在给定的任意m个球中用无码天平称
尽量少的次数，
确保“找出坏球并判定它比好球偏轻还是偏重”了。
为了整体掌握，方便选用，把相关结论列表如下：
说明：
一，关于“
轻重”
1，“已知轻重”、“未知轻重”、“判定轻重”：显然是关于坏球相对于好球而言；
2，“一堆
疑轻，一堆
疑重”：坏球还未知在哪一堆里，但如果在“疑轻”那一堆里的话，坏球就可判定“偏轻”，如果在“疑重”那一堆里的话，坏球就可判定“偏重”；
二，“两堆：一堆疑轻，一堆疑重”中的最大值，是指“每一堆”的。

有了对“找坏球”问题的一般结论，搞清了其中一些本质的东西，我们就可以来探究：在“任意多个”球中“找出坏球并判定它比好球偏轻还是偏重”的
具体操作过程。
通常是这样的
思路：
首先是“三分”，即天平上的“左”、“右”及天平 “下”，称2次后可知坏球轻重（即知道坏球比好球偏轻还是偏重）；
然后就可以利用“已知轻重”那个结论，即：如果已知m个球中的坏球是重（或轻）的，那么，称n次可“找出这坏球”的最大值是3n，就是：3、9、27、81、……。
注意，这实际上有这么一个结论：如果不知坏球是重（或轻）的，那么，称n次可“找出这坏球”。最大值是3n-1，就是：0、3、9、27、81、……。
也就是说：
“不知轻重”比“已知轻重”要多称1次才能找出坏球。
比如，“已知轻重”的
9个球，称
2次即可找出。而“不知轻重”的9个球，“三分”后，需称2次才可确定“疑轻重”的3个球，然后再来1次并判定其轻重，共
3次；
又如，“已知轻重”的
20个球，称
3次即可找出：“三分”为“左6，右6，下8”，称1次后，必能出来“6个知轻重”或“8个知轻重”，都再称2次即可，共3次。而“不知轻重”的20个球，需称2次才可确定轻重（或下面剩2个），然后再称2次找出，并判定其轻重，共
4次；
再如，“已知轻重”的
75个球，称4次即可找出：“三分”为“左25，右25，下25”，称1次后，必能出来“25个知轻重”，再称3次，共
4次。而“不知轻重”的75个球，需先称2次才可确定轻重，然后再称3次找出，并判定其轻重，共
5次。
但是，很多情况下，这个办法（指：“三分”，即天平上的“左”、“右”及天平 “下”，称2次后可知坏球轻重；然后就可以利用“已知轻重”那个结论），
行不通。比如以前详细说过的12个球，39个球就都不行。问题在于，称2次后虽然可知坏球轻重，但不能保证“然后就可以利用‘已知轻重’那个结论”。
这就是“找坏球”问题的难点所在，必须有
新的分组方法以取得突破。
详情待续。