level 3
紫菜♬蛋花汤
楼主
解不出来,大家看看我代码哪里有问题?
问题为:
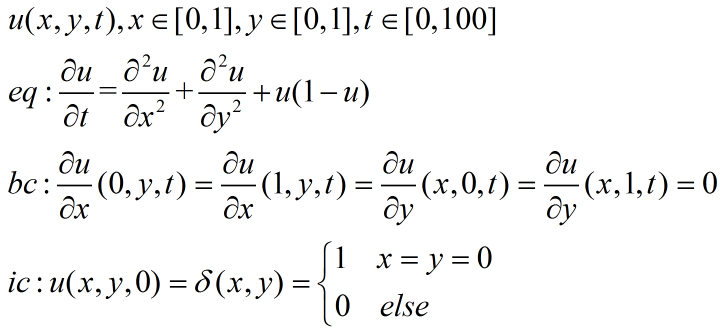
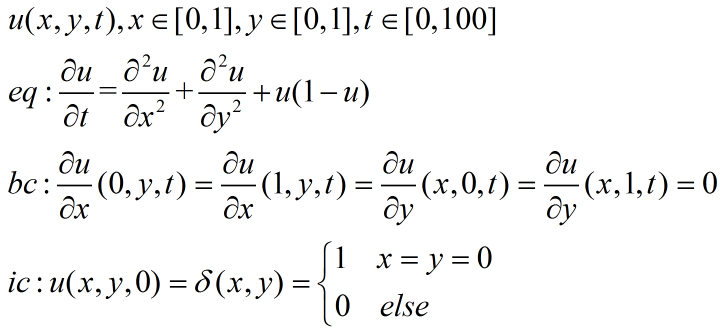 我的代码为:
我的代码为:
rst = NDSolve[
{
D[u[x,y,t],t] == D[u[x,y,t],x,x] + D[u[x,y,t],y,y]+u[x,y,t]*(1-u[x,y,t]),
(*边界条件*)
Derivative[1,0,0][u][0,y,t] == 0,
Derivative[1,0,0][u][1,y,t] == 0,
Derivative[0,1,0][u][x,0,t] == 0,
Derivative[0,1,0][u][x,1,t] == 0,
u[x,y,0] == 0.001 (*初始条件为二维脉冲函数,但是不知道怎么写*)
},
u,{x,0,100},{y,0,1},{t,0,1}
]
Plot3D[Evaluate[u[x,y,t]] /. rst /. x->1,y->1,{t,0,10}] (*作某个点的u关于t的变化图*)
错误提示:
NDSolve::bcedge: Boundary condition (u^(1,0,0))[1,y,t]==0 is not specified on a single edge of the boundary of the computational domain.
没看懂这个错误提示 有没有知道哪里错了~
另外,这个问题的纽曼边界条件用MM这么写对吗?初始条件为二维脉冲函数,只有(0,0,0)这个点为1,其余为0,不太好表达~~
谢谢~^--^
2018年02月22日 11点02分
1
问题为:
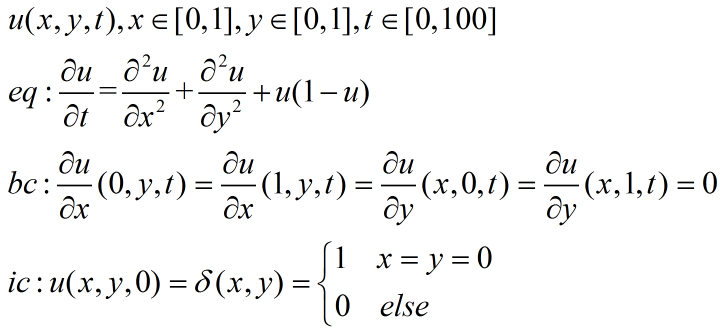
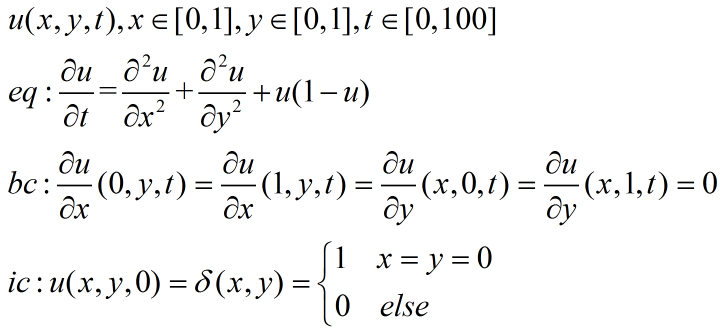 我的代码为:
我的代码为:rst = NDSolve[
{
D[u[x,y,t],t] == D[u[x,y,t],x,x] + D[u[x,y,t],y,y]+u[x,y,t]*(1-u[x,y,t]),
(*边界条件*)
Derivative[1,0,0][u][0,y,t] == 0,
Derivative[1,0,0][u][1,y,t] == 0,
Derivative[0,1,0][u][x,0,t] == 0,
Derivative[0,1,0][u][x,1,t] == 0,
u[x,y,0] == 0.001 (*初始条件为二维脉冲函数,但是不知道怎么写*)
},
u,{x,0,100},{y,0,1},{t,0,1}
]
Plot3D[Evaluate[u[x,y,t]] /. rst /. x->1,y->1,{t,0,10}] (*作某个点的u关于t的变化图*)
错误提示:
NDSolve::bcedge: Boundary condition (u^(1,0,0))[1,y,t]==0 is not specified on a single edge of the boundary of the computational domain.
没看懂这个错误提示 有没有知道哪里错了~
另外,这个问题的纽曼边界条件用MM这么写对吗?初始条件为二维脉冲函数,只有(0,0,0)这个点为1,其余为0,不太好表达~~
谢谢~^--^



