大家好这里是小渊xyz。
最近学到必修四，第二章向量第三章三角恒等变换，两者之间一定有密不可分的联系，于是看到辅助角公式，我就突然想起了一点东西...
以下内容纯属我自己推着玩，如果有人在哪里发现雷同....你咬我啊
先来看这个：这个是余弦差角公式那一章的练习题

这是一个简单的化简题，通常就是直接化简这个式子，有时候还会问问这个函数的单调性极值对称轴周期等等，很明显：
well..可能你觉得这只是一个很简单的题，但是本质是：
也就是说：两个同周期正弦(余弦)函数的和仍然是一个正弦函数，周期都没有变！

这个太神奇了，神奇到我们自然想把这个公式扩充到对正弦函数前的系数到任意实数了！我们来试一试。
这就有点尴尬了，不知道该怎么下手，因为在上一个例子中，2分之根3和1分之2的平方和正好是1，我们才用同角的不同名函数替代了两个数值，把数字化成了角。
很明显，为了我们能够使化简继续下去，我们需要想办法把a和b变成平方和为1
我们先同除以一个n试试
很明显
我们这里n取了正值，取负值也可以，但是负号最后会消掉，因此并没有什么意义。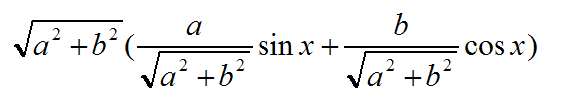
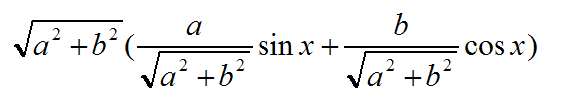我们会得到这个式子，很明显我们设一个角的正弦值和余弦值分别满足下面两大堆东西
恭喜你，这就是大名鼎鼎的辅助角公式。李善兰先生的杰作。
但是这你都知道吧..光说这些就有些太无聊了。

我们来接着往下看。
对于得到的式子，振幅和初相位真是莫名的熟悉，很明显，对于一个，两条直角边分别为a和b的直角三角形，那么很明显斜边是r，其中一个锐角就是θ
比起那个三角形，倒还不如在直角坐标系中，a和b在横轴和纵轴，接着做两个向量a和b的和，其模即使所得sin函数的振幅，夹角θ就是初相位。

这下就有好玩的了，我们把横纵轴定为sin cos -sin和-cos
绿色的分别是sin方向和cos方向的两个单位向量。
那么sinx+cos自然是深蓝色向量，长度是根2，到sin轴的夹角是45°
那么我们可以说sinx+cosx=根2 sin（x+45°）
品红色向量是sinx-cosx，长度是根2，到sin轴的夹角是-45°
那么sinx-cosx=根2 sin（x-45°）
黄色向量是-sinx+cosx 长度是根2，到sin轴的夹角是135°
那么-sinx+cosx=根2 sin（x+135°）
或者也可以这样想，黄色向量到cos轴的夹角是45°
那么-sinx+cosx=根2 cos（x+45°）
换句话说根2 sin（x+135°）=根2 cos（x+45°）这是显然成立的，因为sin（x+90°）=cosx

相量图如下
由相量图和一些简单的几何关系，我们可以得到：
这个不言而喻，但是这是对的？我和我同桌赌一毛钱我是对的。

我们来证明一下
仍然是用了正弦和角公式展开，然后提取sinx 接着就可以套辅助角公式了。
根号下用余弦半角公式（有一些开根号什么的我取了正，因为我们可以把cosθ/2规定在只能取正值的范围内，也就是一四象限），sin里面则是正切半角公式的有理形式的逆用。
这说明相量图是可用的。
（顺便赌赢了一毛钱）

我们来看
下面是用和差化积的步骤，同样能推得同样的结果。
换句话说：
也就是说，用相量图可以证明出和差化积公式，和差化积是a=b=1时的特例。
用相量图还可以画出其它的公式。但是似乎就用处不大了。

事实上每一个向量都可以对应一个有序实数对，那么每一个正弦量都可以用一对数表示
那么，sin轴和cos轴上的，分别是这个向量的正交分解，也就是
很明显对于两个正弦量的加和例如：
对两个振幅分别为A和B的正弦型函数分解，得到四个分别在sin轴和cos轴的向量，使用辅助角公式后开始化简，最后得到一个及其熟悉的公式
为了从几何上理解，咱们还是用三角形法则，很明显那个开根下的东东就是余弦定理而已，式子中好几步的运算其实画一个相量图就十分好理解了。

最后整个式子就可以化成这样的形式。
很明显这个式子才是一个一般式，之前所推的都可以用这个式子表示出来
当A=B=1时，便是12楼的结果，再当其中一个取0时，便是8楼的结果，再当一个在x轴一个在y轴时，便是最之前sinx+cosx的结果了，足以说明以上的各部都是这个公式的特殊形式。

换句话说，我们从代数和几何两个方面算得了两个正弦量相加的情景，我们经历了由特殊到一般，再由一般到特殊的几个步骤。
换句话说，对于两个正弦量的加和
个人感觉还是十分神奇的

帮你顶起来，张渊你真的够了

张渊泥垢

加精哇😂

小渊好厉害