上次的思考题
“对1层嵌套矩阵的所有元素求均值”https://tieba.baidu.com/p/4073612986
被@angelycs 秒破，哎，尽管还是有很多可以深入的探讨余地，但貌似各位只要找到了一个方便的方法之后，就不会再去想其他的解了。我感觉各位还是在追求所谓的标准答案，仍没有脱离应试教育的思维窠臼。
如果我在那一题里说请举出5种不同的编程方法，或许就能把我的意思的传达的更清楚一些吧。
说正题。MC吧里已经有3个提问贴提到了“怎么让MC自动给出任意两条曲线的交点坐标（甚至交点轨迹）”，我这个思考题仅是把那3个提问说得更纯粹一些。
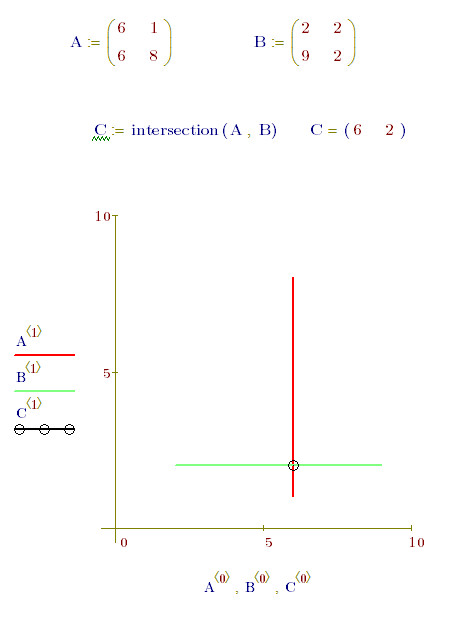
我们在MC中表示线段最常用的方法是组成向量，我举个例子：
在这里A1、B1分别是一个2×2的矩阵，按列提取就成了代表X,Y的向量，绘制这个X,Y向量对，就可以得到1个线段。
为了方便绘图，并把问题具体化一些，我把A1、B1顶点的坐标限制在(0,10)范围内。
嗯，基于连续统，我假设A1、B1的顶点坐标取值范围只要是相同的，就对我们的编程不会产生什么影响。所以咱们暂且规定
这两条线段的两端点坐标X,Y值的取值范围都是(0,10)吧。
这两条线组成的图形千变万化，那么：
（1）请通过编程让MC自己判断出这两条线段是否相交；如果相交，请让MC自己给出交点的坐标；如果不相交，返回(NaN,NaN)。
（2）让MC给出更多的描述信息，比如说：这两条线段的夹角是多少，是否平行、是否垂直，通过无数次的取值之后，这两条线段的长度和的期望值是多少，等等，自己发挥，也可以不回答。
下面这个是我做的初步分析，希望能够为各位的解题提供一些思路吧。

绘图发现相交后，估计还得根据直线方程求解，得到交点。

如果是两条直线，要知道是否有交点，只需判断两条直线方程构成的增广矩阵是否相容即可。
若是两条曲线，则是判断两条曲线方程构成的方程组是否有解，这个不能直接用矩阵来解，用mc的内置函数求解的话，问题就转换成了“在不知道是否有交点且也不知道交点坐标的大概位置时如何准确地估值”。
不知道难点和重点是否在这里？

嗯，我感觉比较有意思的是，当把这个程序编出来，然后运行很多很多次，得到的那个“在一定的取值范围内，任意两条线段的可以发生相交的概率”是多少，可能会得到一个跟π有关的值吧。

@wwwdongliting @angelycs 线段要比直线麻烦一些，比如说：
这两条线段处在一条直线上，但没有交点。更过分的，在一条直线上的两条线段发生了重合，就等于有无数个交点，此时我们应该怎么界定“交点”的定义呢？这得自己发挥。

这题的关键是找思路。
比较暴力的解法是这样的：
可是各位也看到了，需要经过5次if判断！如果用这个方法来解更多条线段相交的问题的话，明显无效率。
我想问的是，有没有什么办法能够简化这个程序呢？能够使其运行的更快一些。

我忽然想到一个方法，可避免定义域不同等很多问题。利用线段的参数方程，每次一条线段，改变参数，动点在线段上移动，同时计算每次到各个线段的垂线的长度，并记录下来。再移动到下个动点，再次计算，并记录到各线段的垂线的长度。再次移动，再次记录。到每个线段的第三个记录与前两个比较，即可判断出在该线段的哪一侧，若由长变短再变长，即可判断有交点。退回去二分法寻找交点。动点再继续前进，重复以上过程。
也可动点一遍走完全线段，记录下到各线段每次的距离。反过来再处理交点问题。

不是平行线的一般情况还是比较方便得到结果的：
但这个方法对于平行线平行线这种特殊情况来说，返回的都是(NaN,NaN)。

嗯，对于平行线，find不收敛，会报错，所以加了一句on error
咱们放大一些。有了这个error分支，就可以比较方便的往里面插“平行线”“共线不重合”以及“共线重合”这三种情况的算法了。

这真是极好的，真是羡慕啊。旁观学习！

判断夹角的话，可以把线段转换成矢量，进行归一化，处理成模为1的两个向量，然后进行一次叉乘，就可以得到夹角的正弦值。

哦，我直接用搜狗拼音也能弄出这个来……
a×b = |a||b|sin(θ)

当两个向量斜率相同的时候，如果截距不同，则是平行线，如果截距相同，则是共线了。
共线的情况比较复杂，有五种情况，如果这个斜率不是垂直于y轴，那么我们就可以通过每个点对x轴的投影，即每个点的横坐标值，来把这个问题简化为一维的排列组合问题。
当这个斜率垂直于y轴的时候，我们可以通过调换向量端点的x，y值，使其平行于y轴，转化为x轴投影问题。如下：
嗯，为方便后面的研究，我们定义一个简单的函数：
这个函数的目的是为了求出两对向量x，y各顶点之间的差的符号的。
嗯，为了保证函数运算结果统一性，首先用sort，因为是线段向量，只有两个顶点，通过sort颠倒了前后顺序之后并不会改变向量本身的性质。
z把y颠倒了一下，是为了方便后面的计算。
将x与y的差和x与z的差放在一个向量里，用sign()函数求值。sign()就是当x＜0时；为-1，当x＞0为1；当x=0时，为0。
由此，可以从两对向量里得到四个不同的数，从而能比较方便看出它们的一维的数值关系。
嗯，下面为了方便图示，我把共线的两条线段上下错开一些。为了方便研究，我使用了简单的例子，对x，y赋值，因为仅讨论的是正负号问题，所以尽量用简单的赋值会使思路更清晰一些。
第1种情况：
第2种情况：
第3种情况：
第4种情况：
第5种情况：
请注意以上5种情况的所得到的向量的和，分别是-4、-3、-2、-1、0。嗯，当B继续向左运动的时候，我们计算allcross(B,A)即可得到0，1，2，3，4了，对应的图形特点是和allcross(A,B)是一样的，也就是说如果我们对这个函数取绝对值，就可以标记不同的一维位置关系了。
但是这里还有一个特例，平行线是线段交叉问题的特例，重合共线是平行线的特例，下面这个两个线段完全相等，就是特例中的特例了：
它所得到的向量和也是0，也就是说，当这个allcross的向量和为0时，我们只要找那个比较短一些向量的两端端点坐标作为重合向量的坐标就可以了。

嗯，有意思的思路！通过矢量计算就能够是三角形的面积有正有负。但是您说的通过两面积的比值确定交点位置，我还不很明白，如果方便，还望您能给出一个例子。:)

如果边长的比值是b，面积比就是b^2，体积比就是b^3 。
知道了面积比，边长比就要开平方。

如果ABC的面积为零，C的坐标就是交点坐标。

实话说，还是没明白。 :(

ABC面积为零，说明ABC共线。而ABD面积不为零，说明D不在线段AB上，线段CD与线段AB的交点就是C 。

按照你说的“面积值异号，或其中一值为零——两线段交叉。”，那么下面的怎么解释？

这道题超麻烦，除了我上面提到的特殊情况之外，还有其他特殊情况。比如说line()函数在向量垂直于x轴的时候不计算，比如说当两个向量互相垂直，且其中一个向量垂直于x轴的时候，更麻烦。
我初步编了一个程序，特么用了5个if，2个on error，总算是把所有可能的分支都铺全了！（因为题目说的是“线段”，不包括“点”，所以我没有考虑当这两个向量里有“点”的情况）
仅做了必要的注释，至于具体某个函数是怎么个意思，各位自己分析，不很难。
预先定义一些函数：
主程序：
用最麻烦的情况做一个验算：
源文件下载：http://1000eb.com/1gjov