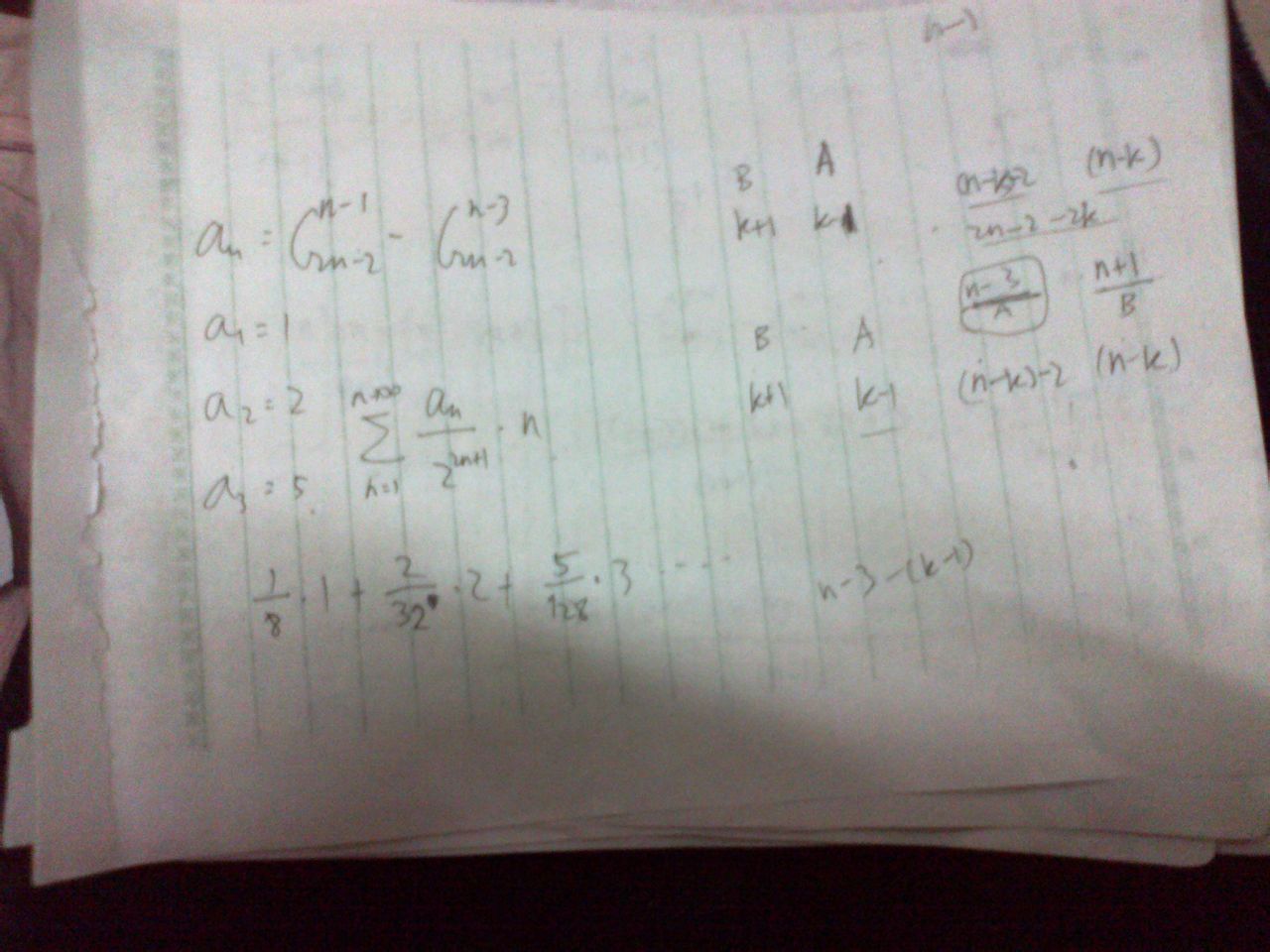几天前在数学吧看到一所谓数学趣题，原题不过高中甚至初中水平，不过是玩点小聪明的把戏。但是喜欢追求挑战和寻根究底的性格使我在原题的基础上稍作修改，考虑更多情况的答案。本来当时就粗算了结果，并发帖以求有同道者一起探讨。本想隔日宣布答案，但不料问题比想象的要复杂，计算数度陷入停滞。直到昨天才刚刚勉强找到了关键数列。

虽然数列找到了，但是求出通项公式却费了不小功夫，而且还是偷懒的规律总结法。在找到通项公式后我也没有急于马上计算，因为我需要找到这个公式的逻辑含义。思考几度陷入困境，我甚至怀疑是否根本没有逻辑含义。其实如果没有最好，这样就能保证没有人能找到比我省力的捷径。但是做数学的学问毕竟是不能凭主观意愿决定问题的，通过不断得思考，我终于找到了它的确切逻辑含义。然后就是非常欣喜顺畅的计算了，非常庆幸高中时候掌握的计算器迭代统计计算技巧还很熟练，单靠纸笔甚至电脑一两天不能完成的计算一个晚上就基本做完了。虽然最后的结果于一开始的设想有契合也有不少出入，但是确实的情况却已经能了然于心了。下面上几张记录了关键思路的草稿图，并作解析。

原题：在一个村子里面，所有的村民都有重男轻女的观念，同时每一度夫妻都会不断的生儿育女，一直到生出一个男孩为止。如果生男孩和女孩的几率是一样的，那么这个村子的最终男女比例应该是多少？
改进1：如果每对夫妇直到生够两个男孩为止，最终的男女比例。
改进2：如果每对夫妇直到生的男孩比女孩多为止（包括只有一个男孩），最终的男女比例。
原题与改进1的情况都很简单，下面都是对改进2的讨论。

我很佩服你！实话！

如果有人能理解我对草图解释中的任意一条，我请他吃饭。如果能理解对第二个草图的解释，我请他吃一周。

这道题作为纯数学问题和应用问题是不一样的。作为纯数学问题，默认了一个隐藏条件，就是每对夫妇都能一直生育，直到达到条件为止，而这个隐藏条件的存在与否不会影响原题与改进1的结果，原因在于他们即使在理想状态下每对夫妇生男孩女孩数量的期望是有限确定的，而且在生有限个孩子与无穷个孩子中，男孩女孩的数量期望总是一样的。比如生一个孩子，男孩的期望是0.5，女孩也是0.5，然后还能算出生两个及以上孩子中，男孩数量的期望和女孩数量的期望也都是0.5。改进1只是将每对夫妇当成原题的两对夫妇来处理。这些都是“没有”问题的。

对于改进2的情况，就没有这样简单了。首选如果每对夫妇生孩子有上限，通过对称原则很容易得出男女1:1的结论。而如果没有这个限制，男女比例必须考虑无穷的情况，虽然无穷的极限也是1:1，但是其意义却不同于前两个，因为每对夫妇生孩子的数量期望是无穷的。所以有意义的计算就是在有生育数量的限制下，满足男孩多于女孩的夫妇男孩与女孩的比例期望。

在生不超过n个孩子的条件下，停止生育夫妇的男孩女孩比例期望为x，以下是在n的各个取值下对应的x：
n=3 x=6:1 ;
n=5 x=3.75:1 ;
n=7 x=2.973156643:1 ;
n=9 x=2.581967213:1 ;
n=11 x=2.33726813:1 ;
n=21 x=1.816897689:1 ;
n=41 x=1.518536028:1 ;
n=201 x=1.20037074:1 ;
n=1001 x=1.086023989:1 .

能打这么多字？？？