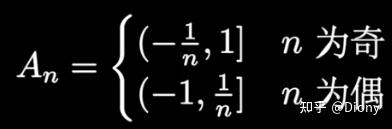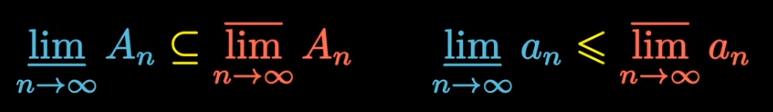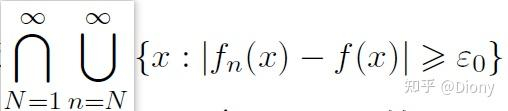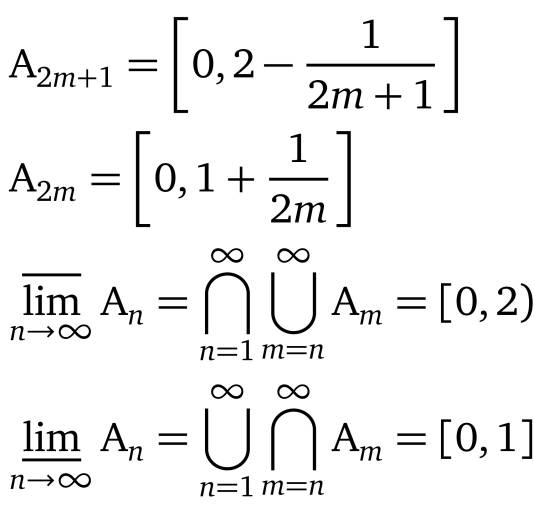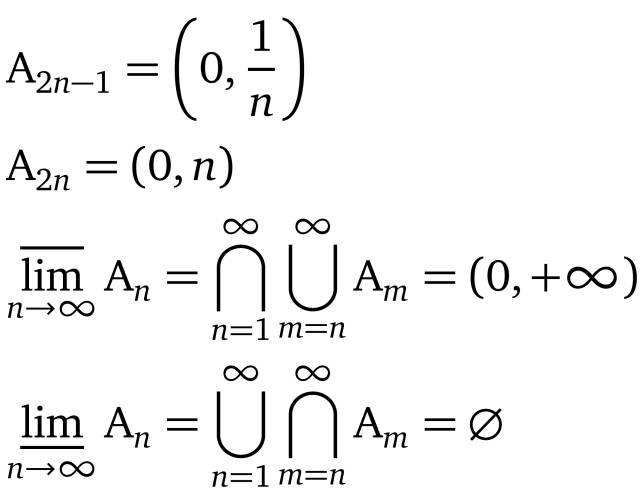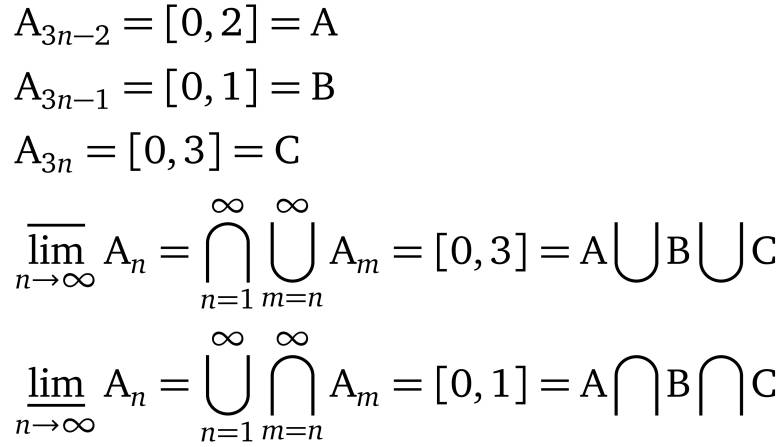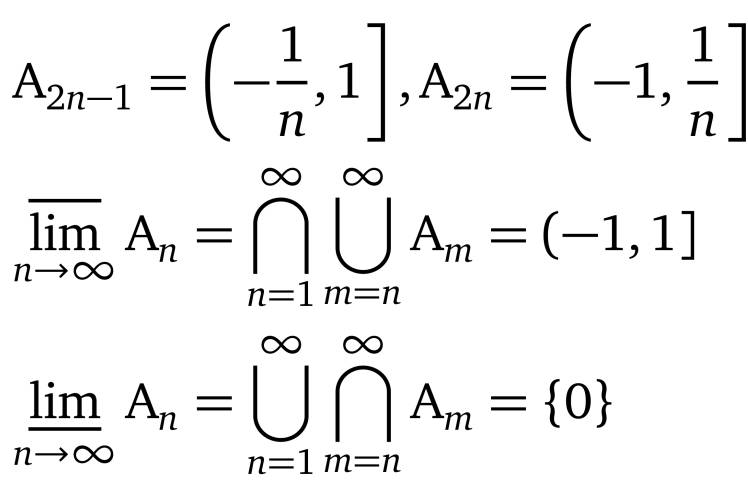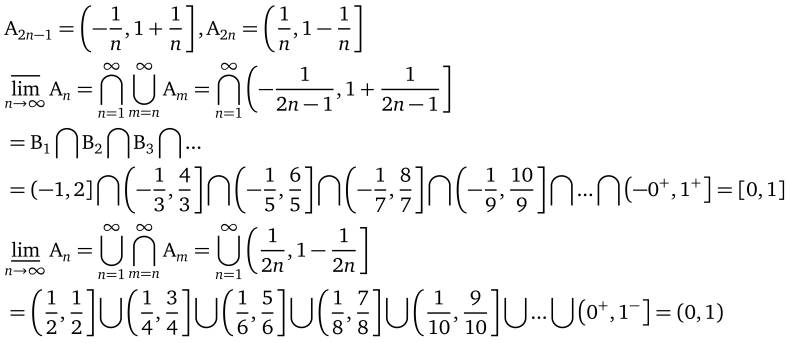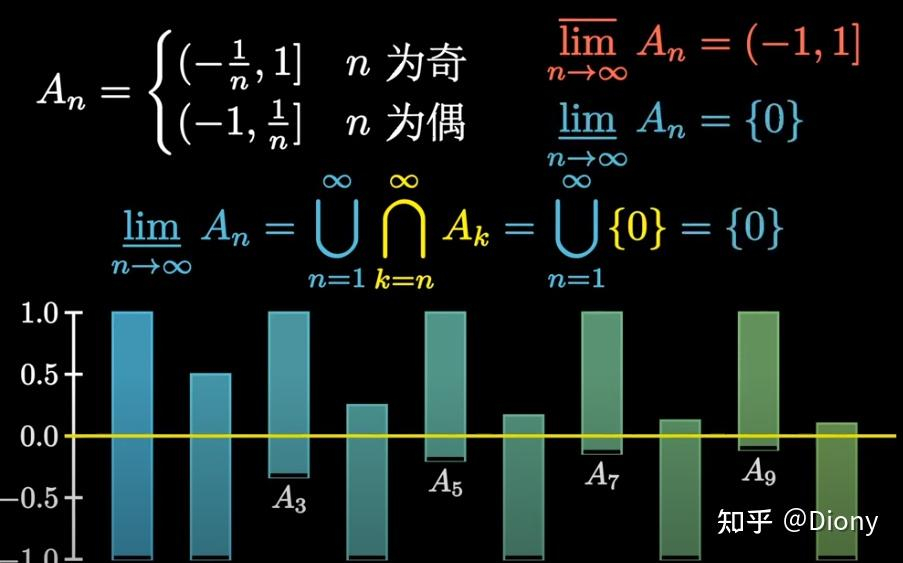
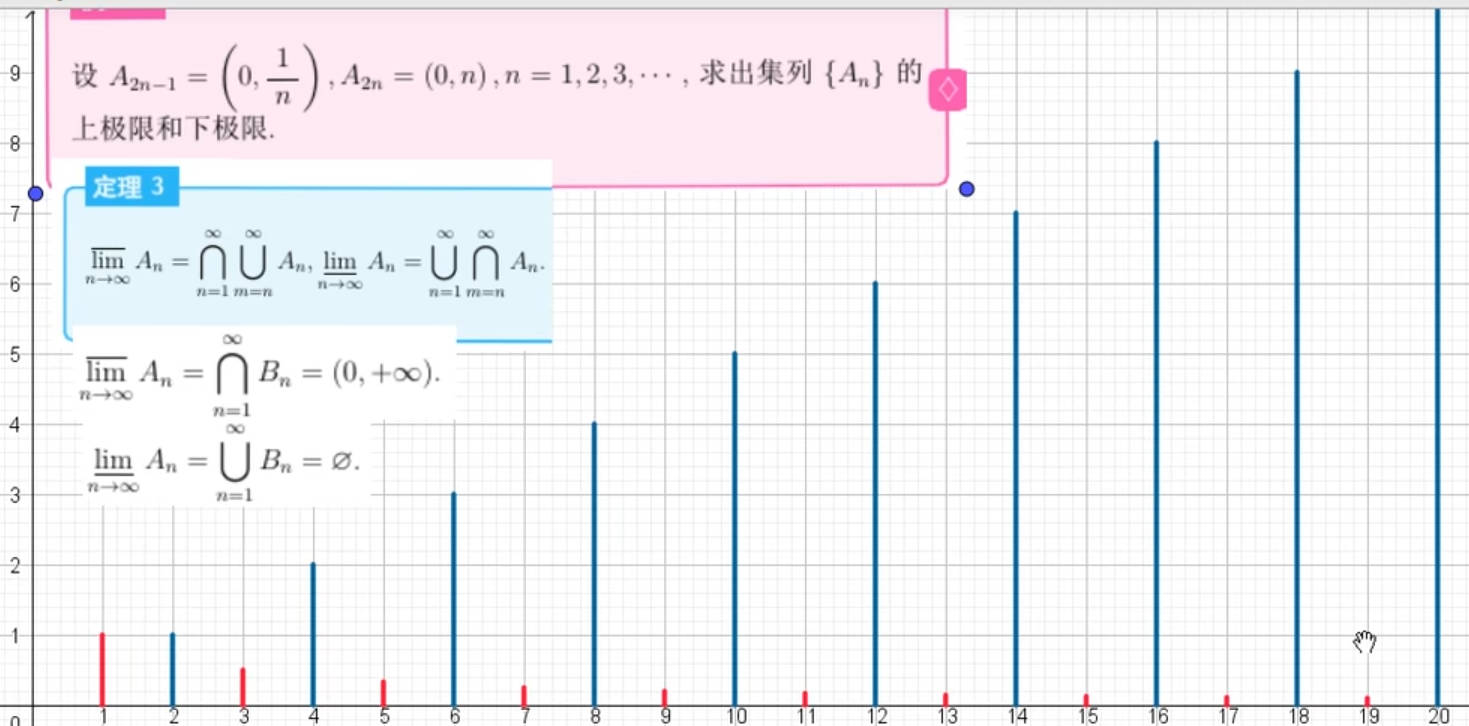
更直观的解释是：
1.={出现无数次的元素}
2.={不仅出现无数次，而且缺席的次数有限}
::
检验一个元素是不是上下极限很简单。想象把所有Ak中的元素叫来开个小会，填一份报告：
1. 是否存在于无限个Ak中
2. 是否不存在于无限个Ak中
那些#1. 中填了否的自己聚在一团，我们不关心（出现次数太少了）。
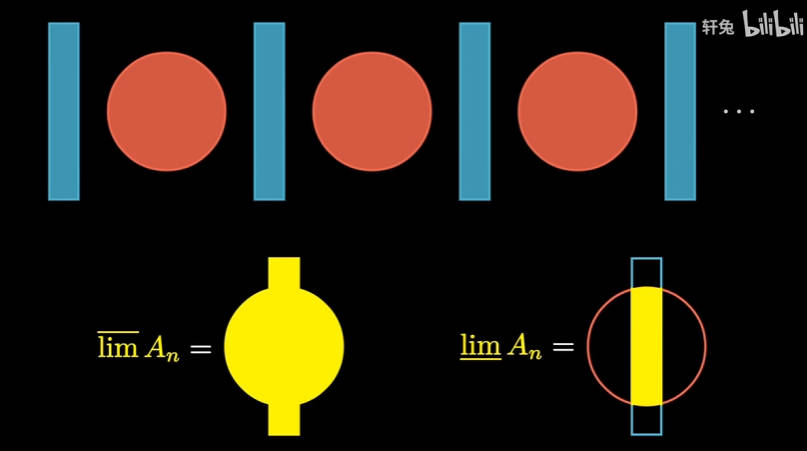
那些#2. 中填了是的待在另一个角落，它们虽然出现的次数很多，但是有无数次缺席。称为“A的上极限集”。
那些#2. 中填了否的待在中间，它们只在前N个集合中不存在，称为“A的下极限集”。
::
好比Ak是你人生中的第k天要去见的人的集合，每个人是一个元素。你决定每天都要见老婆，但是每三天要去跟小三约会。于是你的小三和老婆都是“出现无数次的元素”，均属于A的上极限集；但是你的小三同时也有无数次的缺席（三天一次），而老婆没有一天缺席，于是只有老婆在下极限集。

EX 1:
先算上极限，很明显不管从哪往后看，并集一定包含(-1,1]。
再算下极限，交集的范围要小多了，除了0我们没有把握有其他数字存在。
顺便教一个重要性质：下极限集包含于上极限集，与数列类似嘛。

来一个进阶的题：
x构成的点集D称为非收敛点集。至此，我们已经从数列讲到了集合列，又从集合列讲到了函数列。
首先最外层的k=1到∞可以化掉，因为“大于无穷个1/k的并”相当于是“大于ε”（想多小就多小）。
写成下面的形式：
到这里就结束了，因为设上图这个集合是个集合列，x是属于里边无穷多个集合的。
也就是上极限，是不是结束了？

EX:

EX:

EX:

EX:

EX:

上极限=并
下极限=交