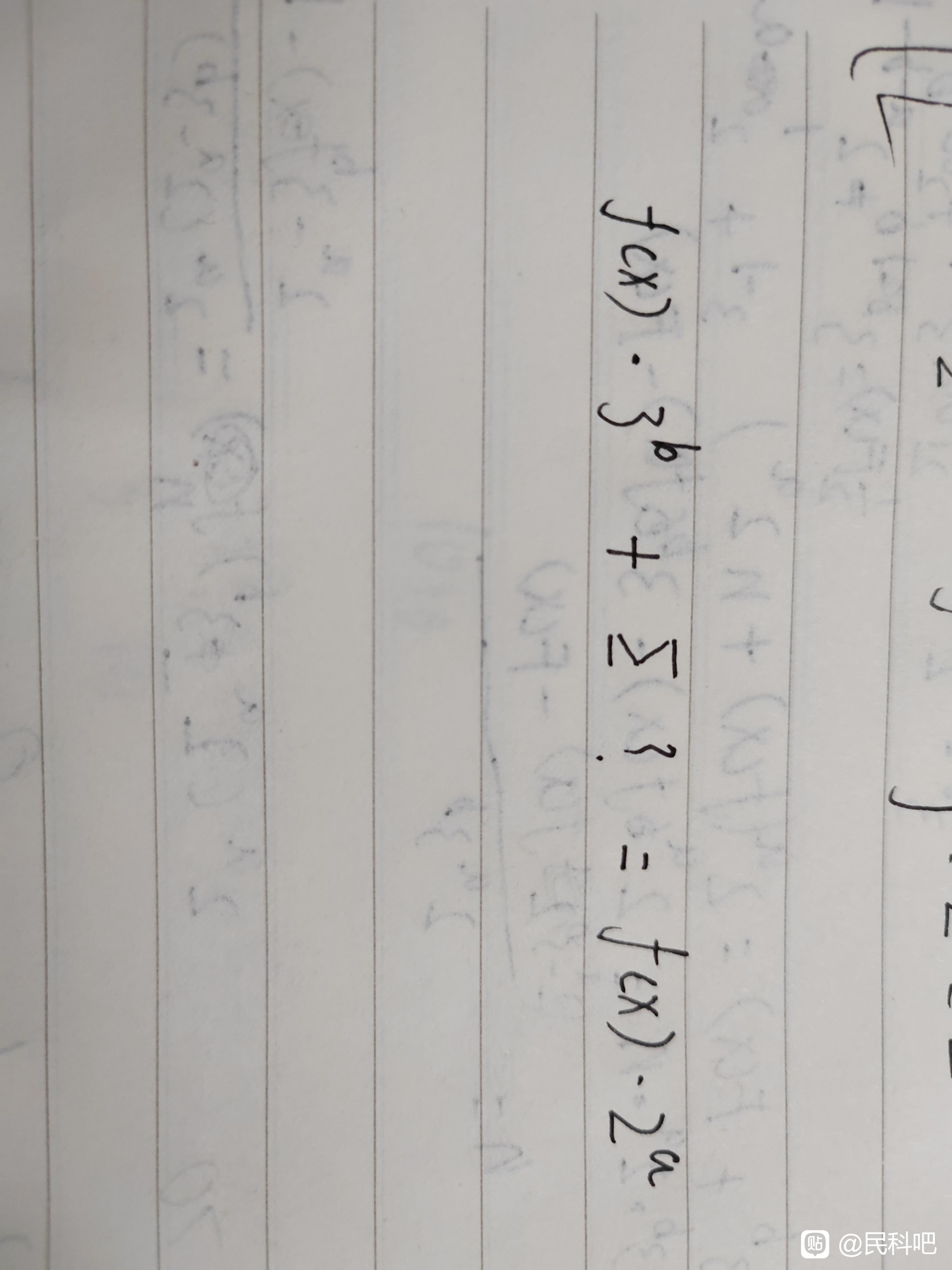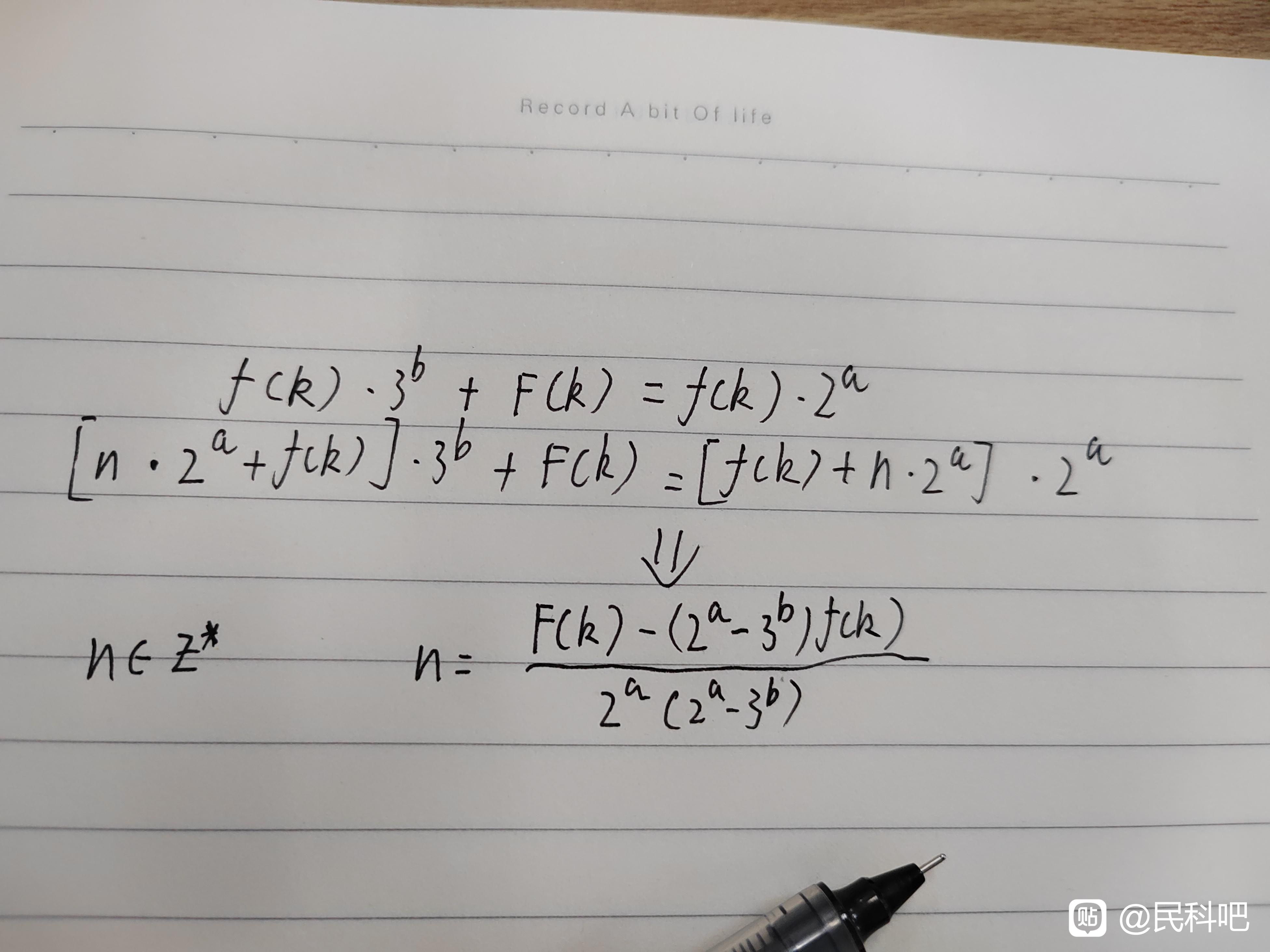在书上看到的一个假说：当一个数为奇数时乘三加一，为偶数时除以二，不断循环，最终都会变为124循环，例5，奇数，乘三加一16，除二，连除二，最终等于一，乘三加一为4除二再除二为一，开始循环。可以试试其它数但你肯定试不出来反例。反例至少大于2^65
它说历史上哪个哪个大科学家没法证明，乐，我想了一个探索的思路，我去翻了一下相关论文，发现好像是全新的，就分享给8u们
我认为某些数可以构成一个全新的循环，我的思路是这样的：对于数k’，它第一步若是乘三加一，计为1，若是第一步除二计为0，那么，数k’可化为一与零的数列，如图一：
这里当数列出现四个0时，就停止计数，不难发现，数1后必是数零，将计一规则改为乘三加一除以二，那么，该数列就有了一个新性质：如图二
不难发现对于2^4以下的所有数k’，它都有唯一确定的数列k与之对应。易推导出，对于2^a以下的任何数，都存在唯一的a位一零组合与之对应，且对于任意n*2^a+k’，其编码k在a位以下完全相同。我的基础想法想完了

顶一下，继续说，若存在循环数列，则对于经过a次运算回到原点的值来说，则可以写为n*2^a+k’，该k’有一与之对应的a位一零数列k，那么，可以设f（k），使得f（k）=k’，当n=0则如图三
数数列中一的个数，计为b，将式子两边同时乘2^a，可得：如图四，不难计算出“？”=3^右侧一的个数*2^左侧数字数，则设F（k）=K
最终我们得到一个方程式：如图五

把完整的过程用数学语言写出来，这样文字描述别人怎么理解你的思路

角谷猜想，好像已经有人证明了，不知道是不是对的

这是角谷猜想，也叫冰雹猜想，目前数学界已知的证明都是错误的，也即这个问题尚未被解决。但陶哲轩在2019年取得了这个猜想的突破性进展，可以大胆猜测这个猜想是成立的，楼主可以去看看相关的论文