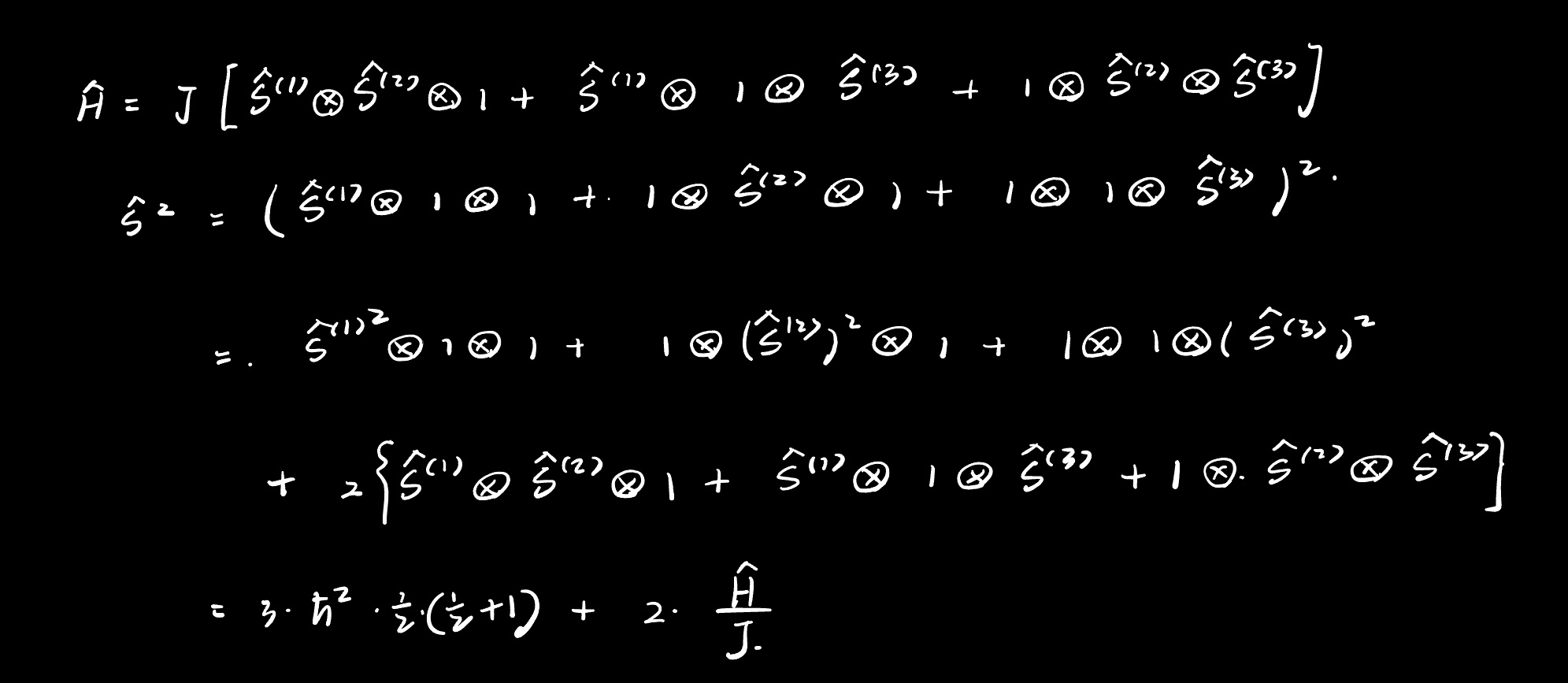请教一道格里菲斯上面的题目，因为是新版所以网上还没有找到答案，希望在吧里有大佬可以解决。
题目的背景就是一个三角形，每个顶点放一个1/2自旋子，因为不能达到相邻自旋相反就会形成阻挫现象，现在哈密顿量就是H=J\sum_{<i，j>}\mathbd{S}_{i}\cdot\mathbd{S}_{j}，要去研究基态能量还有它的简并度。
我的想法是这样的，因为哈密顿量可以改写成H=J/2（\hat{S}^2-9/4*\hbar^2），那能不能把这个体系的波函数就看成|sm>，这样基态就是要让s（总自旋）尽量小，既然是三个自旋子那取1/2就可以了，也就是两上一下或者两下一上，总共的简并度就是6。
因为没有答案所以也不清楚这种想法对不对，网上能找到的和磁阻挫，几何阻挫相关的都是一些晶格里的讨论了，所以还请吧里大神不吝赐教！

召唤一下吧主@Sun_12357 @雨归大海 @不讲理的虾🌿

怎么都没人的

实验方向的看不懂这个

你确定吗？这个体系的希尔伯特空间应该是三个1/2自旋的直积，如果我没记错的话你写的hamitonian是两个的。

前面说的没错，令S最小就行。但这是三个s=1/2的自旋相加，得到的总角动量S可能是S=1/2，3/2。你说的6种态包含了所有m=+-1/2的情况，并不一定是S=1/2。其中一些是S=3/2的态