我希望矩形左右两侧设置周期条件后的效果是，源的位置平移，整个场的分布也平移，但是现在还是会有变化，是我用的方法不对吗？
程序：
\[CapitalOmega] = Rectangle[{-1, -1}, {1, 1}];
{ufun1, ufun2, ufun3, ufun4} = Table[NDSolveValue[{-\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) ==
If[(x - wy)^2 + y^2 <= 1/4, 1, 0],
PeriodicBoundaryCondition[u[x, y], x == -1,
Function[x, x + {2, 0}]],
DirichletCondition[
u[x, y] == 0, (-1 < x < 1 && (y == -1 || y == 1))]},
u, {x, y} \[Element] \[CapitalOmega]], {wy, {0, 0.25, 0.5,
0.75}}];
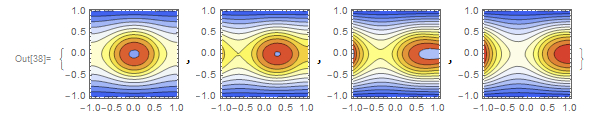
Table[ContourPlot[ufun[x, y], {x, y} \[Element] \[CapitalOmega],
ColorFunction -> "TemperatureMap",
Contours -> Table[n, {n, 0, 0.3, 0.02}],
AspectRatio -> Automatic], {ufun, {ufun1, ufun2, ufun3, ufun4}}]

现在的效果：

按你的设置，边界条件只在x == 2n-1时成立，你要的应该不是这个效果吧。
如果要整个场都具有周期性，要在一整个周期（一个基本单元）内设置周期边界条件。
但是你还有狄利克雷边界条件，而一个点不能同时参与它与周期边界条件，所以应当避开它。
所以，例程中挖半圆出来的做法实际上是必须的。

手机没法测，总之先调调MaxCellMeasure选项试试。