好，来说说浮点数。（每楼都不会太长，防止系统抽风）
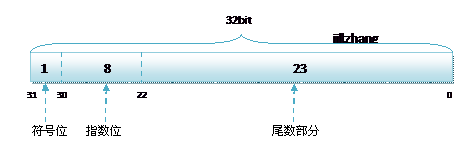
浮点数最直观的感受是它的长度，最常见的有单双精度，不常见的有半精度，四精度，八精度。常见的规格适用几乎于一切编译器，对应的声明是float和double，但是还有一种特殊的long double，如果编译器支持，他是80位的，不支持就会映射到double去。至于128位和256位的四精度，八精度，基本用不到。半精度用于对性能要求很高但对结果精度要求低的场合，比如GPU。

那么，我来讨论float和double的数据结构。
首先一句话建立初步印象：浮点数在计算机中的表示是二进制的科学记数法。
所以，浮点数由：符号位31bit/63bit，阶码23bit-30bit/52bit-62bit，及尾数0bit-22bit/0bit-50bit组成。

插

好久没见过有含金量的帖子了

符号位：整数为0，负数为1；
阶码部分：单精度浮点8位阶码，代表科学记数法的指数部分，不过它的值并不是指数的值，而是再加一个偏移量：0x7F，对于双精度浮点，则是11位阶码，偏移量为0x3FF。
位数部分：对于二进制小数比如1.1010111001，规定小数点前面必须是1，这跟十进制科学记数法一样，小数点前面必须只有一位不为0的数，比如50*10^2是错误的，必须是5*10^3，同理，在二进制下，小数点前面必须是一个1.所以尾数就是二进制数有效数字去掉小数点前面的1.
根据这个我们做一个推断：

6.125该如何表示？
首先，转化为二进制数为：110.001
转化为标准科学计数法为1.10001*2^2
然后开始生成浮点数：首先，是正数，所以符号位为0；其次，指数部分为2，所以阶码部分为0x7F+0x02=0x81；最后，有效数字为1.10001去掉小数点前面的1，只取小数：10001然后后面填充0凑够23位。
把上述结果转化为二进制得：0|10000001|(1)10001000000000000000000其中：|表示结构分割，()表示1被舍弃。
十六进制为：0x40C40000，将结果代入浮点转整形程序得：6.125

技术贴，顶一下

单双精度浮点能表示的范围远比相同位数的整形数大得多。但是相比于整形数，某些位用作表示符号和阶码，所以有效数字位数降低，即牺牲精度换表示范围。
对于float，最大值为：1.11111111111111111111111*2^128;
对于Uint32，则为：2^32;
甚至对于Uint64，则：2^64也没能超过它，更不用提double了！
现在来说第一部分：浮点和整点互转

C函数原型：float Uint64ToFloat(Uint64 Op1,Uint64 Op2)
其ASM源码为：

实现思路：
Uint64长度为两个字，最长为64位，最短为0位，其中高位字也可能为0。等等比较多的情况。
对于这个转换其实不难，算法先探明传入参数的有效数字位数，位数通过计算前导0数间接得出，由于前导0只是一个字长内的结果，所以对大于32位有效数字和小于32位有效数字分开处理。见8-13行。
接下来对传入参数有效数学位数与几个关键值做比较，决定算法流向。当大于等于特征值时分支成立，并同时得到实际位数与特值差。见14-17行。
对于小于24位的参数，需要左移补位，凑出24位有效数字位数并取23位尾数，见18-23行;
对于大于24位却小于56位的参数，需要右移丢弃，并将最后丢弃一位舍入。同样凑出相同的有效数字位数。该操作需要传入参数的高低位字，见24-28行;
对于大于56位参数，直接对高位字移位舍入即可，见29-36行。
其中每一个分支还实现最终结果组装及函数返回。

其实楼主你不觉得浮点数的这个结构可以用于优化对数运算吗

汇。。。汇编？