月城的工作表太棒了!尤其是那个递归的程序,若搞一个“MC花式编程大赛”,这个估计能中头奖。
LNS问的不清楚MC使用了什么算法,比较运算的结果,我感觉MC的内置算法用的就是连分式法。
我大概算了一下运行时间:


从上图可知:
除了MC内置算法外,循环法用的时间最少。
confrac法,因为MC调用符号计算,相当于是引用了外部程序的dll,尽管是安装在同一个根目录下,但调用dll需要走windows的dllkernel,定位注册表键值后,将程序调出计算,然后再重新定位注册表到MC的数值计算界面进行程序板的计算,给出结果,这里绕了一个弯儿,所以即便是内置算法,计算速度也是有些慢的。MC进行符号运算的其他运算也是在这里卡。它的最好成绩是0.075s,最差成绩是0.094s。
循环法,用for break组合,这要较while快,因为不用调用boolean计算的dll文件,也是少走了很多弯路。它的最佳成绩是0.046s,和MC的内置算法相当了!最差成绩是0.078s。
递归法,在返回嵌套函数值的时候,多次遇到if,因为在这个程序里使用了好几个递归,每个递归都要调用dllkernel一次,算起来就显得慢一些了。它的最好成绩和confrac法时间相同,最差成绩是0.101s。
MC内置算法,就是在结果上双击,在“数字格式”菜单里选分数,并给出精度级。
从上面的例子可以看出,MC的内置函数的精度级控制并不是很理想的,有好几个重复答案,而在月城文件中可以看出,在相应的精度级处是有另外的更好的答案的。
因为MC内置算法是用C语言编写的,相比MC的解释语言本身就运行快很多,但从这个结果中看,首先结果质量不如用MC编程的效果好,其次运算速度并没有明显优势。我感觉很有可能MC内置算法使用的也是递归法结构。
它的最好成绩是0.046s,最差成绩是0.047s,发挥比较稳定,这是编译语言的特点。
综上所述,就像原来zpz老师指出的,用MC自己编程序不但可拓展函数的功能,运算效果更好,而且运算速度不一定就比编译语言的慢。
非常感谢月城的这次出色的表演!

 这么处理的时候,得到的小数点后面的数跟乱码差不多了…… :(
这么处理的时候,得到的小数点后面的数跟乱码差不多了…… :(
 这么处理的时候,得到的小数点后面的数跟乱码差不多了…… :(
这么处理的时候,得到的小数点后面的数跟乱码差不多了…… :(


 从上图可知:
从上图可知: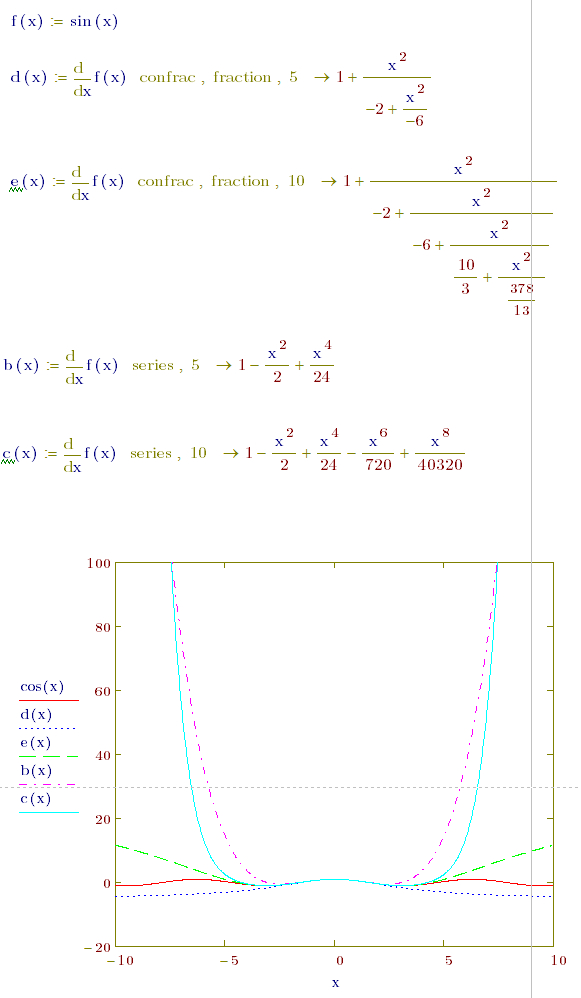
 不过用confrac控制精度更直观一些,而且可以直接处理标量,而series需要将标量放在一个表达式里,然后在表达式里再想办法还原这个标量。比如说e,直接confrac,fraction就可以了,可在series中,需要写成e^x,然后series,x=1,才可以。
不过用confrac控制精度更直观一些,而且可以直接处理标量,而series需要将标量放在一个表达式里,然后在表达式里再想办法还原这个标量。比如说e,直接confrac,fraction就可以了,可在series中,需要写成e^x,然后series,x=1,才可以。