level 1
level 1
吧务
level 12
只画平面图的话很简单,一句代码就行
ContourPlot[-0.33781 x^2 + 2*0.189161 x y - 0.381768 y^2 + 2*0.460866 x + 2*0.410426 y + 1 == 0, {x, -2, 8}, {y, -2, 7}]
要画动态图的话就比较麻烦了,需要解微分方程,而且中间有许多推导过程
严格算的话大致步骤是这样的:
先把一般方程化为极坐标方程(取一个焦点为原点),然后把极坐标方程代入动量矩守恒的式子,得到φ的一阶微分方程,然后解出φ,代入方程得到ρ,就可以绘制动画了
其中最麻烦的地方是怎样确定动量矩的值:如果小行星质量和太阳质量都是已知的话当然可以很轻松地算出来,但如果没有这两个量的话,求起来就比较费劲了,起码我是没想出来怎么求
但是这道题可以用一个偷懒的方法糊弄过去——反正动态模拟只要比例对就行,动量矩的值不影响速度之间的比例,所以直接取成1就行,极坐标方程也可以这样耍赖,反正只要离心率对了形状就对了,具体尺寸就可以不管了
代码如下:
eqn = -0.33781 x^2 + 2*0.189161 x y - 0.381768 y^2 + 2*0.460866 x +
2*0.410426 y + 1;
{a, b, c, d, e} =
Coefficient[eqn, #] &@{x^2, x y, y^2, x, y} /. {x -> 0, y -> 0};
{xc, yc} = {(b e - 2 c d)/(4 a c - b^2), (b d - 2 a e)/(4 a c - b^2)};
{A, B} = {Sqrt[(2 (a xc^2 + c yc^2 + b xc yc - 1))/(
a + c + Sqrt[(a - c)^2 + b^2])], Sqrt[(
2 (a xc^2 + c yc^2 + b xc yc - 1))/(
a + c - Sqrt[(a - c)^2 + b^2])]};
\[Phi]0 = 1/2 ArcTan[b/(a - c)];
eq = 1/(1 + Sqrt[A^2 - B^2]/A Cos[\[Phi] - \[Phi]0]);
sol = NDSolve[{\[Phi]'[t] (eq /. \[Phi] -> \[Phi][t])^2 ==
10, \[Phi][0] == 0,
WhenEvent[\[Phi][t] == 2 \[Pi], end = t;
"StopIntegration"]}, \[Phi], {t, \[Infinity]}][[1]];
Animate[
Show[
PolarPlot[eq, {\[Phi], 0, 2 \[Pi]}, Axes -> None],
Graphics@
{{PointSize[Large], Green,
Point[p = {(eq /. \[Phi] -> \[Phi][t]) Cos[\[Phi][
t]], (eq /. \[Phi] -> \[Phi][t]) Sin[\[Phi][t]]} /. sol]},
{PointSize[0.05], Orange, Point[{0, 0} /. sol]},
{Dashed, Line[{{0, 0}, p}]}}
], {t, .01, end}]
其中椭圆各参数的求法来自
http://wenku.baidu.com/view/84aae46e783e0912a2162a88?fr=prin
里面的式子都是可以推导出来的只是有些麻烦
也可以参考下
http://mathematica.stackexchange.com/questions/51654/an-easier-way-to-find-the-properties-of-an-ellipse-from-its-equation/51663#51663
https://tieba.baidu.com/p/3078253810?pid=51527625479&cid=0#51527625479
这两个帖子
最后效果大概是这样的
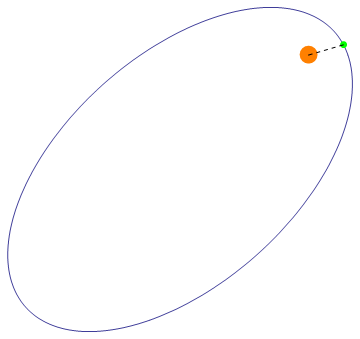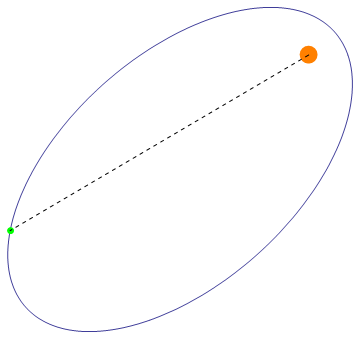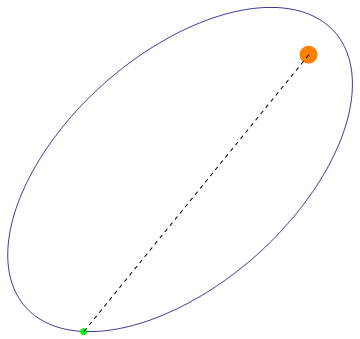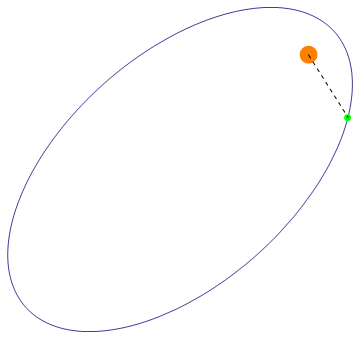

2014年07月22日 08点07分
4
ContourPlot[-0.33781 x^2 + 2*0.189161 x y - 0.381768 y^2 + 2*0.460866 x + 2*0.410426 y + 1 == 0, {x, -2, 8}, {y, -2, 7}]
要画动态图的话就比较麻烦了,需要解微分方程,而且中间有许多推导过程
严格算的话大致步骤是这样的:
先把一般方程化为极坐标方程(取一个焦点为原点),然后把极坐标方程代入动量矩守恒的式子,得到φ的一阶微分方程,然后解出φ,代入方程得到ρ,就可以绘制动画了
其中最麻烦的地方是怎样确定动量矩的值:如果小行星质量和太阳质量都是已知的话当然可以很轻松地算出来,但如果没有这两个量的话,求起来就比较费劲了,起码我是没想出来怎么求
但是这道题可以用一个偷懒的方法糊弄过去——反正动态模拟只要比例对就行,动量矩的值不影响速度之间的比例,所以直接取成1就行,极坐标方程也可以这样耍赖,反正只要离心率对了形状就对了,具体尺寸就可以不管了
代码如下:
eqn = -0.33781 x^2 + 2*0.189161 x y - 0.381768 y^2 + 2*0.460866 x +
2*0.410426 y + 1;
{a, b, c, d, e} =
Coefficient[eqn, #] &@{x^2, x y, y^2, x, y} /. {x -> 0, y -> 0};
{xc, yc} = {(b e - 2 c d)/(4 a c - b^2), (b d - 2 a e)/(4 a c - b^2)};
{A, B} = {Sqrt[(2 (a xc^2 + c yc^2 + b xc yc - 1))/(
a + c + Sqrt[(a - c)^2 + b^2])], Sqrt[(
2 (a xc^2 + c yc^2 + b xc yc - 1))/(
a + c - Sqrt[(a - c)^2 + b^2])]};
\[Phi]0 = 1/2 ArcTan[b/(a - c)];
eq = 1/(1 + Sqrt[A^2 - B^2]/A Cos[\[Phi] - \[Phi]0]);
sol = NDSolve[{\[Phi]'[t] (eq /. \[Phi] -> \[Phi][t])^2 ==
10, \[Phi][0] == 0,
WhenEvent[\[Phi][t] == 2 \[Pi], end = t;
"StopIntegration"]}, \[Phi], {t, \[Infinity]}][[1]];
Animate[
Show[
PolarPlot[eq, {\[Phi], 0, 2 \[Pi]}, Axes -> None],
Graphics@
{{PointSize[Large], Green,
Point[p = {(eq /. \[Phi] -> \[Phi][t]) Cos[\[Phi][
t]], (eq /. \[Phi] -> \[Phi][t]) Sin[\[Phi][t]]} /. sol]},
{PointSize[0.05], Orange, Point[{0, 0} /. sol]},
{Dashed, Line[{{0, 0}, p}]}}
], {t, .01, end}]
其中椭圆各参数的求法来自
http://wenku.baidu.com/view/84aae46e783e0912a2162a88?fr=prin
里面的式子都是可以推导出来的只是有些麻烦
也可以参考下
http://mathematica.stackexchange.com/questions/51654/an-easier-way-to-find-the-properties-of-an-ellipse-from-its-equation/51663#51663
https://tieba.baidu.com/p/3078253810?pid=51527625479&cid=0#51527625479
这两个帖子
最后效果大概是这样的

