首先一看去可以注意到


,
做个变量代换y=arctanx,则有:x=tany。
再注意到


。
我们可以把两个数列写成:


两边求极限,只需要证明后面那个积分为0即可。
问题的关键来到求tany的n次方的积分,相信这个在大学里数学老师应该会教,就算没教做作业估计都做过……但是,不出意外我们考完试就不会记得,於是楼主不出意外也就不记得了……
但是没关系,我们现在不是考试,所以我们尽情地问度娘吧。度娘上的高人说:


我们这里依样画葫芦,可以有:


,也就是:
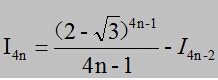
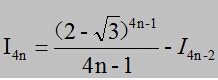
,
两边求极限,中间那项分子是小数的无穷次方,分母是个无穷大,自然就等於0,所以我们知道n趋於无穷时,
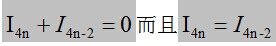
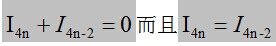
也就是


,有了这个结果,就可以证明:


接下来证明3.141<π<3.142.直觉上估计也是取n等於某个具体数,问题是取多少呢?我们要相信日本的老师也是有人性的,所以n不会是太变态的东西,所以不妨从小开始逐一尝试.
由於时间关系,直接告诉大家,n=2时:
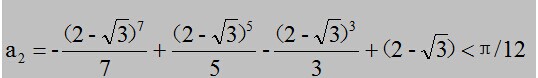
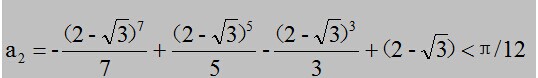
,
同时乘以12,得到:π>3.14158>3.141,成功证明左边。
至於右边,n=1,12b1=3.14175>π,从而有π<3.142.
至此,证明终了,Q.E.D。
感想:狱门塾果真名副其实的狱门塾,这题反正楼主高中绝逼做不出……



 ,
, 。
。
 两边求极限,只需要证明后面那个积分为0即可。
两边求极限,只需要证明后面那个积分为0即可。
 我们这里依样画葫芦,可以有:
我们这里依样画葫芦,可以有:
 ,也就是:
,也就是: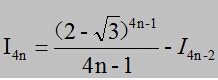
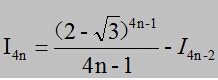 ,
,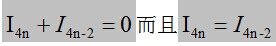 也就是
也就是 ,有了这个结果,就可以证明:
,有了这个结果,就可以证明:
 接下来证明3.141<π<3.142.直觉上估计也是取n等於某个具体数,问题是取多少呢?我们要相信日本的老师也是有人性的,所以n不会是太变态的东西,所以不妨从小开始逐一尝试.
接下来证明3.141<π<3.142.直觉上估计也是取n等於某个具体数,问题是取多少呢?我们要相信日本的老师也是有人性的,所以n不会是太变态的东西,所以不妨从小开始逐一尝试.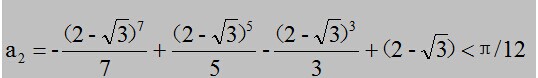
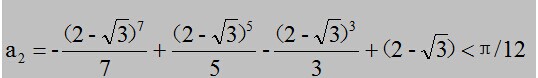 ,
,