无论怎样都是旧题了，大家无聊时做做看……

1、怎样把一块正四面体形状的蛋糕均匀地分成5块，同时使表面上的奶油也分得均匀？
注：奶油薄厚的误差忽略不计。

第1题附加题：
怎样把一块矩形蛋糕均匀地分成5块，同时使表面上的奶油也分得均匀？
注：矩形蛋糕即长方体形状的蛋糕，奶油薄厚的误差仍忽略不计。

2题、除了圆形井盖不会掉到井里去之外，请试着找出其他形状的井盖使之不会掉进井里去。
注：本题多解，找出一种答案即可。

3题、有一可剪裁的国际象棋棋盘，将其左上角和右下角的方格剪掉。问能否把剩下的62个方格，剪成31个长为2、宽为1的长方形呢？
注：长为2——2格的边长和；宽为1——1格的边长。本题为快速解答题。

4题、聪明的晶晶爱动脑筋，常产生一些新的想法．一次妈妈给他10元钱去买东西，他把这10元钱分成10份，分别包在10个小纸包里，他想，从1分到10元，不管这次花多少钱，我都可以从这10包中挑出几包来付钱，不再麻烦售货员叔叔、阿姨找钱了，有这种可能吗？

5题、已知一个打乱了的魔方。你能找到方法，把另一个魔方也打乱得和已知魔方一模一样吗？

　　抱歉，第2题需要附加的限制条件如下：
　　1、一般情况下是井盖和井口的形状相同，而井盖比井口稍微大一些。
　　2、井盖的厚度会影响对本题的分析，请正在思考的朋友们理解为井盖比较薄。
　　话说用金属茶叶盒（或筒）的盖子来说明这个问题更合理些。
附第2题原题：
除了圆形井盖不会掉到井里去之外，请试着找出其他形状的井盖使之不会掉进井里去。
注：本题多解，找出一种答案即可。

▲附加思考题1、
把正方形面积平均分成4份的方法有：
1、分成四个小正方形；2、分成四个等腰直角三角形。
请考虑其他分法。

▲附加思考题2、
把正三角形面积平均分成3份的方法，一般是分成三个钝角等腰三角形。
请考虑其他分法。

▲附加思考题3、
把正三角形面积平均分成4份的方法，一般是分成四个小的正三角形。
请考虑其他分法。

▲附加思考题4、
请考虑把正方形和正三角形面积平均分成5份的方法。

▲附加思考题5、
请考虑把任意长宽的矩形面积平均分成5份的方法。

▲附加思考题6、
增加难度：请在兼顾周长也5等分的情况下，考虑把任意长宽的矩形面积平均分成5份的方法。

下周只能每天晚上来上网回复答题的各位了……

其他没人做的题， 貌似没人感兴趣哦……一会儿我发井盖那题的答案，可以么可以么？

1、先设定关于多边形的两个概念（称谓）：多边形的“宽度”与“直径”。
　　1>设想从不同角度用两条平行直线来夹着任意一个多边形。角度不同，这两条平行线之间的距离也不相同。某个角度，这个距离会最小。把这个最小距离叫做这个图形的“宽度”。
　　2>根据“圆的直径是它的最长的弦”的规定，也可以把任意三角形的最长边、还有任意其他多边形最长的对角线，都叫做“直径”。
　　3>图形的宽度不可能比直径大！
2、只要盖子的宽度小于直径，那它就会掉下去。
　　比如：正方形的“直径”是对角线，大于它的“宽度”（边长），会掉下去；
　　正三角形的“直径”是边长，大于它的“宽度”（高），也会掉下去；
　　其他所有凸多边形都可以用比较“直径”与“宽度”大小（长短）的方法来判断……
　　五星形是个凹十边形。凹的多边形或不规则形状，与凸的形状情况有些不同，但仍可按比较“直径”和“宽度”的方法来判断。
　　只有当宽度和直径相等时，盖子才不会掉下去。
3、常宽度图形。
　　要是图形的宽度和直径相等，这样的图形叫做“常宽度图形”。
　　圆是最常见的常宽度图形。
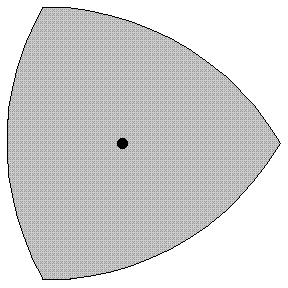
　　此外，常宽度图形还有三角拱形（Reuleaux三角形）、正五角拱形、正七角拱、正九角拱……无限个图形。
　　三角拱形是以正三角形的三个顶点为心，以它的边长为半径，画三段圆弧得到的。
　　正五角拱形是以正五边形的五个顶点为心、再以对角线为半径画五段弧得到的，它比较像圆但实际上不是圆。
　　只要是一个边数为奇数的等边图形，都可以把它“加工”成常宽度图形。
　　所有常宽度图形的盖子都不会掉下去。
　　◆下边附一张常宽度图形：Reuleaux三角形

本帖的无聊题就做到这里……没解决的么……没解决的题目就滚动到下期好了！
那么，周末再见……

十五字
十五字十五字十五字十五字十五字